Presentation of a Uniform Spheroform Tetrahedron

Patrick Roberts, September 21, 2011, Corvallis, Oregon

Background

Spheroform solids have the property of 'constant width'. Tangent parallel planes on opposite sides of the solid will maintain the same separation distance no matter how the solid is oriented. The simplest example of a solid of constant width is the sphere.

The study of spheroform tetrahedra begins with the Reuleaux tetrahedron, named by analogy to the Reuleaux triangle, described by German engineer Franz Reuleaux, 1829-1905. The Reuleaux tetrahedron is the solid formed by the intersection of four spheres, having their centers located at the four vertices of a regular tetrahedron, and having radii equal to the edge length of the tetrahedron. Each face is a section of sphere surface.

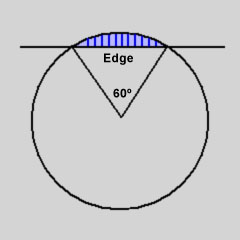
The Reuleaux tetrahedron is not quite a solid of constant width. Distances measured through opposite edges are slightly greater than the edge length of the interior tetrahedron.

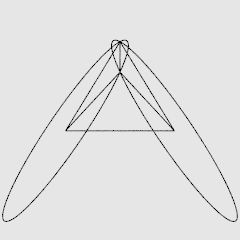
Swiss mathematician Ernst Meissner showed in 1911 that some of the edges could be altered to form a true solid of constant width. A spindle-shaped surface is formed by the revolution of a section of circle arc around its chord. This shape replaces three of the tetrahedron's six edges. There are two possible arrangements for this replacement. Three modified edges can meet at a vertex, or three modified edges can be placed around one face. Both of these arrangements satisfy the condition that opposite pairs of edges are always of different type.

The Meissner tetrahedra lack the symmetry of uniform polyhedra since their edges are not all identical.