Presentation of a Spheroform Solid with Tetrahedral Symmetry

Patrick Roberts, September 21, 2011, Corvallis, Oregon

Background

Spheroform solids have the property of 'constant width'. Tangent parallel planes on opposite sides of the solid will maintain the same separation distance no matter how the solid is oriented.

The study of spheroform tetrahedra begins with the Reuleaux tetrahedron, named by analogy to the Reuleaux triangle. The four faces of the Reuleaux tetrahedron are sections of sphere surface, each centered on its opposite vertex.

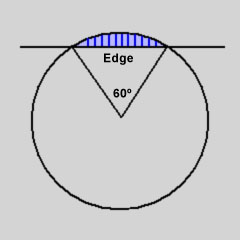
The Reuleaux tetrahedron is not quite a solid of constant width. The width between opposite edges is slightly greater than the width between vertex and face.

Swiss mathematician Ernst Meissner showed in 1911 that some of the edges could be altered to form a true solid of constant width. A spindle-shaped surface is formed by the revolution of a section of circle arc around its chord. This shape replaces three of the tetrahedron's six edges. There are two possible arrangements for this replacement. Three modified edges can meet at a vertex, or three modified edges can be placed around one face. Both of these arrangements satisfy the condition that opposite pairs of edges are always of different type.

The Meissner tetrahedra lack complete tetrahedral symmetry since their edges are not all identical.